[나의 개발일지] - KD-Tree With C++

KD Tree 개요

우리가 Lidar 센서뿐만 아니라 이미지 검색, 딥러닝, 데이터 마이닝, 과학 시뮬레이션과 같은 응용 프로그램을 사용할 때 주로 활용되는 알고리즘이 있습니다. 바로 KD Tree인데요, 간단하게 정의하면 K 차원 즉, 2차원이나 3차원에서 분포되어있는 데이터들을 효율적으로 저장, 관리하는 자료 구조입니다.

KD Tree는 특히 Point Cloud에서 Object의 특징들(Plane, Edge 등등)을 탐색할 때 유용하게 활용할 수 있습니다. 물론 가장 간단한 방법은, 모든 데이터의 위치 정보를 Array에 저장하고, 전체 Point Cloud Data를 탐색해서 찾을 수도 있습니다. 하지만 매 순간 매 Point에 대해 검색하면 시간이 오래 걸립니다. 따라서 공간을 나누어 탐색하면 좀 더 빠르게 접근할 수 있습니다.

KD Tree의 아이디어는 각 데이터를 트리와 같은 구조로 나누어서 저장하는 것입니다. 이진 트리를 사용해서 관리하게 되죠. 그럼 나중에 데이터를 찾고 사용하고 싶을 때 비슷한 데이터끼리 모여있어서 찾는 시간을 최대한 단축할 수 있습니다. 대표적으로는 자율주행의 인지 쪽에서 특정 객체를 찾고자 할 때 유용하게 활용됩니다.

KD Tree 원리

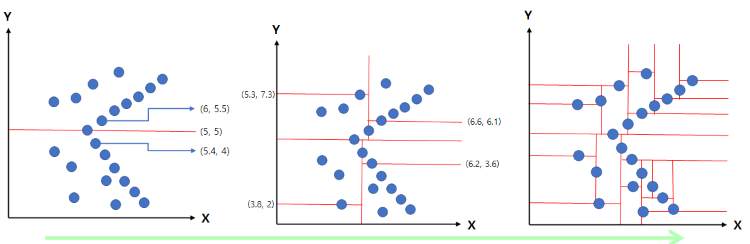
랜덤으로 Point들이 산란되어있는 공간이 있다고 가정해봅시다. KD Tree는 이 Point들을 서로 연결해주는데, 그 구조는 이진 트리와 같습니다. 트리 개념으로 접근하면 자기보다 작은 데이터는 왼쪽에, 큰 데이터는 오른쪽에 정렬합니다. 그림과 같이 설명 들어가겠습니다.

KD Tree를 진행할 땐 보통 Center에 가까운 Point가 Root(기준)가 됩니다. 그 후, Root Point와 근처에 있는 Point 들을 비교하죠. X축을 기점으로 작으면 왼쪽, 크면 오른쪽으로 이동하면서 가까운 Point를 찾고 연결합니다. 그다음은 Y축이 기점이 되고 -> X축 -> Y축…. 이렇게 진행되죠. 이후에 찾을 Point가 없다면 끝내게 됩니다. 일반적으로 코드에서는 재귀 함수를 사용하기도 하죠.

3D KD-Tree

KD Tree는 기본적으로 2D, 3D로 나누어집니다. 2D는 상하/좌우에 따라서 나뉘게 됩니다. 반대로 3D는 좌우/상하/앞뒤에 따라서 나누어집니다.

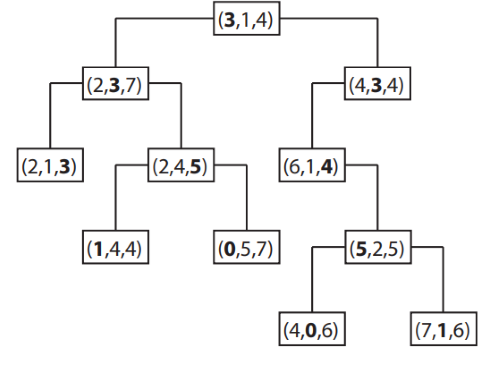
위의 Tree는 X→Y→Z→X 순으로 연결이 진행됩니다. 3D KD-Tree에 대한 설명은 다음 Post에 진행하도록 하겠습니다.

KD Tree 예제

KD Tree 예제 코드

예제 코드의 Readme.md를 보면, 시나리오 0과 1이 적혀있습니다. 시나리오 0은 Random Points를 생성해서 KD-Tree를 진행하는 것이고, 1은 샘플 데이터(.pcd)를 불러와서 KD-Tree를 진행하는 것입니다. 사용 방법은

Scenario 1

먼저 첫번째로 코드를 실행하면 아래와 같이 진행됩니다.

Choose Senario. 0=sample, 1=pcd. ex) Choose: 0
(input) Choose: 0
Choose the Width & Height. ex) W&H: 500 500
(input) W&H: 500 500
Choose the Random Points. ex) Points: 100
(input) Points: 300

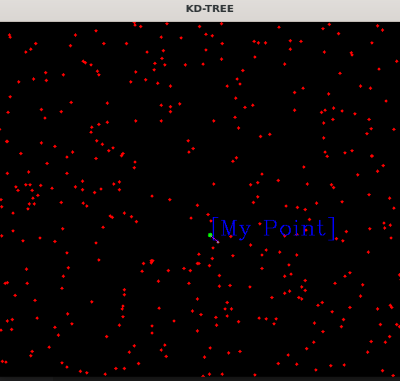
Scenario 2

다음 두번째로 코드를 실행하면 아래와 같이 진행됩니다.

Choose Senario. 0=sample, 1=pcd. ex) Choose: 0
(input)  Choose: 1
Select Position for fine nearest point in width: 1614, height: 1034
Example -> Point: 300 300
(input) Point: 1000 400
(input) Choose the K Points: 100

이며, KNN이랑 같이 코드가 작성되어 있어서 KD-TREE만 먼저 확인해본다면

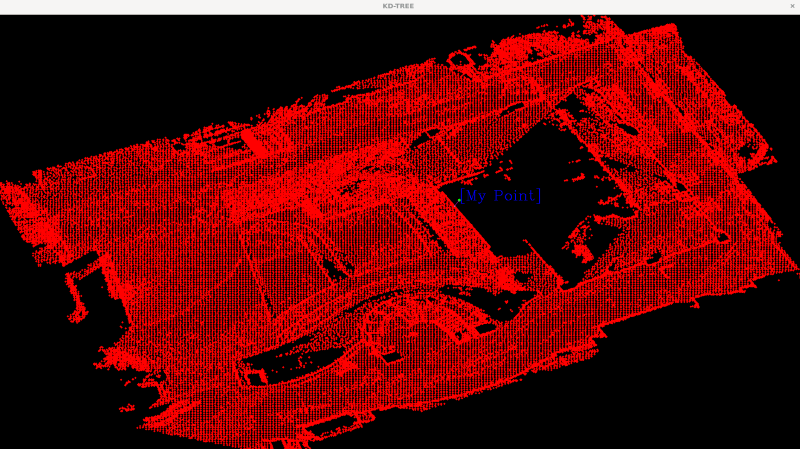
위 사진처럼 출력이 되는 것을 확인할 수 있습니다. 다음은 KD-Tree로 정렬된 자료를 바탕으로 KNN을 진행해보도록 할께요.

참고

Paper: Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation

Github: gishi523